Írjunk játékot! – three.js

Régóta foglalkoztat a three.js függvénytár, amivel WebGL alapú 3 dimenziós tartalmat lehet generálni. Egy korábbi kedvcsináló posztomban bemutattam, milyen széles is a felhasználhatósága, de szerettem volna valami konkrét megvalósítási példát is hozni az alkalmazására. Számos ötlet közül első körben egy egyszerűbb játék megvalósítását tűztem ki célul, bízva abban, hogy sikerül szemléltetnem a dolog egyszerűségét.

Alapkoncepció

Nemrégiben véletlenül ráakadtam a Play Store ajánlatát böngészve a Star Drives játékra, aminek az egyszerűsége nagyon megtetszett. Kifejezetten alkalmas is arra, hogy egy low-poly verzió szülessen belőle, amit böngészőben is lehet játszani.

• Kell két egymást keresztező röppálya egy-egy bolygóval
• Egy űrhajó, aminek a sebességét tudjuk a fel-le gombokkal változtatni
• Ellenfelek, amikkel nem szabad összeütköznie
• Egy kör a bolygó körül egy pontot ér
• A cél, hogy minél több kört tudjunk teljesíteni ütközés nélkül.

Megvalósítás

Akár a nulláról is elkezdhettem volna megírni az egészet, egy keresést mégis megejtettem a githubon és rátaláltam egy egyszerű boilerplate-re, ami a játék több „képernyős” megvalósítását elősegíti, ha mást nem is. Hozzá kell tenni, hogy a boilerplate megoldása nem teszi lehetővé a three.js inspector használatát, így egyszerre tettem szert előnyre és hátrányra, mivel az egyes modellek összerakása eléggé pepecs munka. A következőkben a fontosabb részeket taglalom, némi kóddal, és külön-külön megtekinthető pen-ekkel.

Modellek

A modellek mindegyike egyszerű geometriákból összerakott test. Egyszerűségük miatt választottam ezt a megoldást és el szerettem volna kerülni a külső objektumok betöltését.

Az újrafelhasználhatóság miatt egy külön Models objektumba tettem őket, ami ugyan lehetne szebb, de felhasználás tekintetében így is tökéletes. Az objektum a következő módon épül fel, elkülönítve külön fájlba:

var Models = {
    materials : {
        material1 : new THREE.MeshStandardMaterial( {color: 0xfefefe} ),
        material2 : [ ... ],
        material3 : [ ... ],
    },
    spaceShip : function(){
        var spaceShipModel = new THREE.Group();
        [ ... three.js code ... ]
        return spaceShipModel;
    },
    satelliteOne : function(){
        [ ... ]
    }
}

var spaceShip = Models.spaceShip();
scene.add(spaceShip);
       

A bolygók létrehozásakor már előttem volt a koncepció, mivel régebben ráakadtam erre a pen-re. A röppálya kirajzolásával kellett kiegészítenem őket, amit a következő kódrészlet oldott meg:

var segment = 100, radius = 30;
var lineGeometry = new THREE.Geometry(),
    vertArray = lineGeometry.vertices,
    angle = 2 * Math.PI / segment;
for (var i = 0; i <= segment; i++) {
  var x = radius * Math.cos(angle * i);
  var y = radius * Math.sin(angle * i);
  vertArray.push(new THREE.Vector3(x, y, 0));
}
lineGeometry.computeLineDistances();

lineMesh = new THREE.Line(lineGeometry, new THREE.LineDashedMaterial({ color: 0x6484b7, dashSize: 1, gapSize: 1 }));

Hogyan is néz ki egy „bolygó” köré téve? Itt tudod megnézni..

Az űrhajó kitalálásakor előtérbe helyeztem, hogy alapvetően low-poly modellt szeretnék, semmiképpen sem egy külső betöltött, 3D modellezőben elkészített valamit, így valahogy hitelesebb az egész és amúgyis szimpatizálok a rajzfilmekben látott megvalósítással.

A modell nagyrészének kialakítása viszonylag egyszerűen megoldható volt a three.js „primitív geometriáival” (CylinderGeometry és BoxGeometry). Kisebb csavar akkor jött az elemek összeállítása során, amikor nem szabályos téglatestet kellett létrehozni. Ebben az esetben a mesh létrehozása előtt a drótváz (BoxGeometry) vertex-eit kell manuálisan módosítani, ami abszolút nem bonyolult, és pár soros megoldással a megfelelő alakzattá torzítható a váz. Egy téglatest esetén könnyű dolgunk van, hiszen alapesetben 8 pont határozza meg azt, ami egy 8 elemű tömbnek felel meg. A tömb minden egyes eleme egy-egy vertex, ami x,y,z koordinátákkal rendelkezik, így szabadon módosíthatjuk azokat:

var object = new THREE.BoxGeometry( 2, 9, 2 );
object.vertices[4].y -= 1; 
object.vertices[4].x -= .5; 
object.vertices[5].y -= 1;     
object.vertices[5].x -= .5;
object.vertices[6].y -= 1; 
object.vertices[6].x += .5; 
object.vertices[7].x += .5;
object.vertices[7].y -= 1; 
object.needsUpdate = true;

A kész űrhajó:

See the Pen threejs low-poly spaceship by Zoltan Toth (@totya24) on CodePen.

A bolygók és az űrhajó mellé még szükség van ellenfelekre is, amik műholdak formájában jelennek meg. A változatosság kedvéért kettőt is csináltam, a lehető legegyszerűbb módon, szintén „primitív objektumok” összerakásával.

Játéktér – scene

A boilerplate támogatja az egyes játékállapotokat, így könnyen elkülöníthető a kezdőképernyő, maga a játék és a játék vége állapot, ráadásul ezek között gyorsan lehet váltani is.

A kezdő és végállapot részletezését nem tartom fontosnak, igazából minkét esetben egy-egy modell van kiemelve, a végén pedig latod, hány pontot szereztél (azaz hány kört tettél meg) és ha az nagyobb a localStorage-ben eltárolt maximumnál, akkor jelzi hogy rekordot döntöttél.

A játékot megvalósító állapot is alapesetben két részre osztható. Inicializálás és a játéklogikát megvalósító loop. Az inicializálás során a következő történik:

• elhelyezem a bolygókat a röppályákkal
• létrehozok egy „kontrollpontot”, amin az űrhajó áthaladása jelent egy teljesített kört
• a röppályára kezdőpozícióba helyezem az űrhajót
• lenullázom a pontokat és az egyes segéd-számlálókat
• definiálom a tömböt, ami az ellenfeleket tárolja majd

Objektumok animálása

Az objektumok animálása értelem szerűen már a loop-ba kerül, ami mindaddig tart, amíg nem ütközöl egy ellenféllel, de ezt később részletezem.
A bolygók esetében egyszerű forgatásokról van szó, és hogy látványos legyen, a bolygó és a körülötte lévő „wireframe shield” eltérő irányba mozog.
Az űrhajó animálása két részre bontható, egyszer mozog egy körpályán, közben pedig a lángcsóváját is mozgatja.

A körmozgás megvalósítása:

this.movement += this.multiplier; // sebesség
this.spaceShip.rotation.z = -1 * (Math.PI / 180 * this.movement) + 0.08; // forgatás
this.spaceShip.position.x = -1 * 350 * Math.cos(Math.PI / 180 * this.movement); // pozíció
this.spaceShip.position.y = 350 * Math.sin(Math.PI / 180 * this.movement) - 100; // pozíció

A sebességet a this.multiplier változó határozza meg, ami a lenyomott gombtól függően (fel, le, semmi) 0.5, 1 vagy 2 lehet. A sebesség változtatásával oldom meg az egész játék lényegét, azaz, hogy minél tovább elkerüld a műholdakkal történő ütközést. A * this.movement* egy segédszámláló, ami egyesével növekszik (360-at túllépve nullázódik, de csak a hibakeresés elősegítése érdekében). Gyakorlatilag ez határozza meg, hogy a körpályán milyen szögben áll az űrhajód és ennek megfelelően pozicionálod. A mozgatás mellett mindig irányba is kell forgatni a hajót, hogy előre nézzen, ezt a második sor oldja meg egy kisebb korrigálással. A pozicionálást végző sorokban az egyes szorzók a körpálya sugarát határozzák meg.

A lángcsóva mozgatása sincs túlbonyolítva. Mivel adott egy (kvázi) 0-360 közötti érték, adja magát a szinusz-hullámú mozgás:

var multiply = Math.sin(step*30 * Math.PI / 180) + 1; 
this.spaceShip.children[1].scale.set(this.flameMultiplier,1+(multiply * 0.05),this.flameMultiplier);
this.spaceShip.children[1].position.y = multiply*2.05;

A fenti kódban a step szintén egy segédváltozó, ami egyesével növekszik, és látszik még, hogy nem az egész spaceShip objektumot változtatja, hanem csak egy részét, konkrétan egy 3 elemből álló, lángcsóvát. Mivel a scale alapértelmezetten az objektum közepétől számolva növeli a méretet, szükséges a pozíció korrigálása is, hogy a lángcsóva kiindulópontja fix állapotban maradjon.

Játékmechanika

Az animáláson túl akad még feladat, hogy a játékból játék legyen. Azt, hogy mikor mivel és mi történjen szintén a loopban határozom meg, a végtelenül egyszerű interaktivitást is belevéve, hogy a felhasználó megnyomta-e a felm, vagy le gombot. A loopban történő folyamatokat az alábbi folyamatábra szemlélteti vázlatosan:

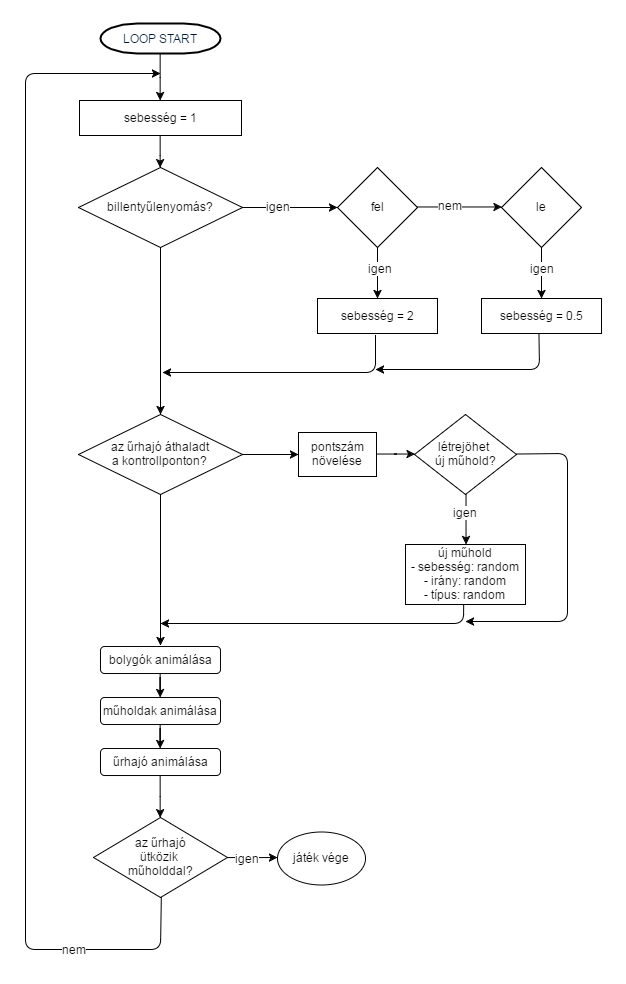
Érdemes pár kiegészítést tenni a fenti ábrához, a részletek miatt. Az új műholdak létrehozásának elég egyszerű a logikája. Azért ez a csavar, hogy némi fokozat kerüljön a játékba:

• ha a pontszám 1
• ha a pontszám 13-nál kisebb és oszható 3-mal
• ha a pontszám 12-nél nagyobb és osztható 5-tel

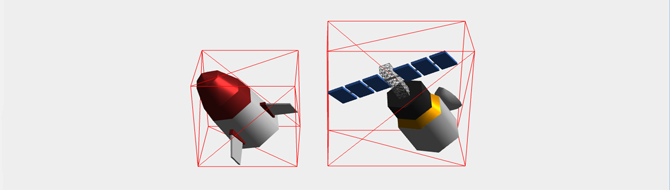
Az ütközések vizsgálata a three.js beépített funkcióink köszönhetően relatíve egyszerű, viszont ha növelni akarom a precizitást, akkor az már pluszmunkát igényel. A three.js kezel egy „speciális” geometriát, ami Box3 névre hallgat. Ez tulajdonképpen egy két térbeli pont által meghatározott téglatest, ami lehetőséget ad arra, hogy megvizsgáljam, hogy átfedésben van egy másik Box3 típusú téglatesttel avagy nincs. Az ütközés vizsgálata a műholdakat bejárva minden esetben lefut a következő kód szerint:

var spaceShipBox = new THREE.Box3().setFromObject(this.spaceShip);
var collosion = spaceShipBox.intersectsBox(new THREE.Box3().setFromObject(this.satellite[index]));
if(collosion){
    game.setState('endgame'); 
}

Érdemes megemlíteni, hogy a fenti esetben két elég elnagyolt bounding box ütközését hasonlítja össze, ami a játék folyamán olyan helyzeteket teremthet, hogy mi úgy látjuk, nem ütköztünk a műholddal, matematikailag mégis, és vége a játéknak. Ezt úgy lehet pontosítani, ha nem a teljes objektumot veszem alapul a Box3 generálásához, hanem csak például az űrhajó testét, így nem növelem feleslegesen az ütközési holttereket egy esetleges antenna vagy apró objektum miatt, ami térben nem foglal el nagy helyet, mégis drasztikusan megnöveli a befoglaló téglatest (bounding box) területét.

A végeredmény

A cikkhez elkészült játék eléggé kezdeti állapotú, de minden hiányosság és bug ellenére játszható.
Ezen a linken próbálhatod ki, de ha a kódra vagy kíváncsi, elérhető a projekt githubon is, frissítése hamarosan várható.

Sajnos a játék még nincs mobilra optimalizálva és a kód is erősen refaktorálás után kiált:)

Jó szórakozást hozzá, remélem sikerült hasznos információkat átadnom, esetleg felkeltenem az érdeklődésed a téma iránt. A kommentek között várom a kérdésed vagy észrevételed!